Calculus Exam
Gave the first exam already. Instead of giving four exams, each with a review day, and a bunch of quizzes, I'm giving eight exams this semester in calculus class. Today's was on anti-derivatives, indefinite integrals, Riemann sums, rectangle approximations, and basics of definite integrals. The only techniques of integration that we know are remembering the derivative rules, the power rule backwards, and find the area.
Class average was a B. Low B if you use the mean, almost a B+ if you use the median.
Lots of students who took calculus in high school were tripped up by the exam. Despite being told TWICE that a "find the area of a semi-circle" definite integral would be on the test (and having a similar problem assigned for homework), some of them tried to fake their way through it with a substitution. No one tried trig subs; trig subs is a BC technique, and the calculus they had in high school was almost all AB. Zero points for badly evaluating that.
People who weren't coming to class didn't hear me say, "on the exam you will need to accurately state FTC2." There went five more points. No pity for anyone who missed that question. When I tell you exactly what's going to be on the test, it's in your best interest to believe me.
One point off for every missing +C. Just because that's traditional.
Most alarmingly, my students couldn't evaluate
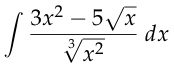
Way too many of them subtracted the denominator from the numerator and then integrated term-by-term. Is that better or worse than the ones who divided the anti-derivative of the numerator by the anti-derivative of the denominator? And how does that compare to the ones who invented a quotient rule for integration?
And the position, velocity, acceleration problem had a non-constant acceleration. Just because you want a(t) to be -9.8 doesn't make it so. And those equations you learned in your non-calculus-based physics class? They don't apply here. There's a reason why we use calculus on these problems.
We'll see how much my message has gotten through: This is not your high school calculus class. You'll need to really know calculus in order to do well in this class.
Class average was a B. Low B if you use the mean, almost a B+ if you use the median.
Lots of students who took calculus in high school were tripped up by the exam. Despite being told TWICE that a "find the area of a semi-circle" definite integral would be on the test (and having a similar problem assigned for homework), some of them tried to fake their way through it with a substitution. No one tried trig subs; trig subs is a BC technique, and the calculus they had in high school was almost all AB. Zero points for badly evaluating that.
People who weren't coming to class didn't hear me say, "on the exam you will need to accurately state FTC2." There went five more points. No pity for anyone who missed that question. When I tell you exactly what's going to be on the test, it's in your best interest to believe me.
One point off for every missing +C. Just because that's traditional.
Most alarmingly, my students couldn't evaluate
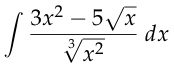
Way too many of them subtracted the denominator from the numerator and then integrated term-by-term. Is that better or worse than the ones who divided the anti-derivative of the numerator by the anti-derivative of the denominator? And how does that compare to the ones who invented a quotient rule for integration?
And the position, velocity, acceleration problem had a non-constant acceleration. Just because you want a(t) to be -9.8 doesn't make it so. And those equations you learned in your non-calculus-based physics class? They don't apply here. There's a reason why we use calculus on these problems.
We'll see how much my message has gotten through: This is not your high school calculus class. You'll need to really know calculus in order to do well in this class.
![Do You? I [heart] Wool. Do You?](http://img.photobucket.com/albums/v314/rudbeckiahirta/iheartwool_88x37.gif)

